Emilio Martínez Pañeda
BEng, MEng, MSc, PhD
Research Projects
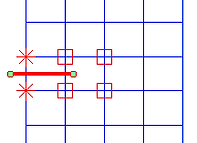
PHENOMENOLOGICAL HIGHER ORDER MODELING OF SIZE EFFECTS IN METAL PLASTICITY
Analytical development and numerical implementation of novel phenomenological higher order formulations to describe the mechanical behavior of metals at small scales. Modelization of the experimentally observed change in material response with diminishing size within the continuum level. Towards an efficient and robust numerical scheme for strain gradient plasticity theories.

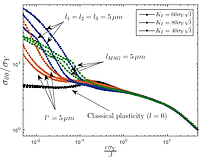
CRACK TIP MECHANICS WITHIN STRAIN GRADIENT PLASTICITY
Continuum crack tip characterization accounting for the local hardening promoted by plastic strain gradients. Development of finite element frameworks to investigate the role of geometrically necessary dislocations under finite strains and rotations. Quantification of the magnitude of stress elevation predicted from mechanism-based and phenomenological strain gradient plasticity theories with respect to conventional plasticity. Assessment of the implications of the plastic size effect in the modelization of several damage mechanisms.
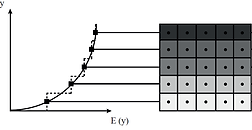
FRACTURE MECHANICS IN FUNCTIONALLY GRADED MATERIALS
Modelization of crack initiation and growth in functionally graded materials. Computation of fracture parameters and assessment of crack propagation criteria. Development of subroutines to introduce the material property variation at the element level in commercial FE packages (ABAQUS). Study of novel methodologies to numerically reproduce the experimentally characterized elastic gradient.
MODELIZATION OF HYDROGEN ASSISTED CRACKING IN HIGH STRENGTH STEELS
Numerical modelization of hydrogen embrittlement in high strength steels. Development of hydrogen-influenced cohesive zone formulations to model the initiation of environmentally assisted cracking. Investigation of the influence in hydrogen diffusion of the increased dislocation density associated with large gradients in plastic strain near a crack.
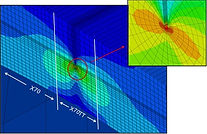
ADVANCED NUMERICAL TOOLS FOR MICROMECHANICAL FRACTURE ASSESSMENT
Development of advanced numerical methodologies for the modelization of crack tip mechanics across the scales. Enrichment of X-FEM formulations to capture the stress-dominated asymptotic field intrinsic to plastic strain gradients. Multiscale numerical modeling of size effects in metal plasticity beyond finite elements.